Making Game Theory Easy With Simple Shortcuts

Over the past few weeks, we’ve been looking at an introduction to game theory in poker with a special emphasis on avoiding math. We have been looking extensively at a very specific type of situation over the past couple of weeks where a player bets all-in on the river against a single opponent. We looked at formulas for the unexploitable strategies, and we looked at how the unexploitable strategies could be used as a beacon to guide our play when trying to exploit players. One complaint has been that it’s difficult to do these calculations at the table, even though they are simple fractions, and that complaint is valid for the most part. That’s why we’re going to focus on simple shortcuts for making this stuff work for you.

The Bluffing and Folding Frequencies

The above chart shows a simple way to recall from memory the unexploitable bluffing and folding frequencies for the three most common post-flop bet sizes as long as you can remember the five values in the middle. There are three arrows connecting sets of numbers on this chart. The first arrow is for a half pot sized bet, the second is for a bet between 2/3 and 3/4 pot, and the last is for a bet that is the size of the pot. For each set of numbers connected by arrows, the bluffing frequency is on the left and the folding frequency is on the right.

Note: This includes an approximation for the folding frequency against a 3/4 pot bet that is close enough to be of good use as a shortcut at the table.

For example, suppose you wanted to know the unexploitable frequencies in a situation where there’s a half pot sized bet being shoved. The left value for that arrow is .25 and the right value is .33, so the bluffing frequency is 25 percent and the folding frequency is 33 percent.

This pulls a lot of information into a very small format that a lot of people will be able to remember without much effort. However, as broken down as this is, it can be made even easier.

The Folding Frequency is the Most Important Value

The folding frequency is pretty useful to know since it tells you exactly how much the calling player will have to call of his or her entire range to be unexploitable, and that’s relatively easy to use as a reference point. The bluffing frequency, however, is fairly useless in practice because it only tells you the percentage of your final betting range that should be bluffs. Thankfully, there’s a solution for this.

Some people have realized that the folding frequency in these situations is the same as the alpha value, or simply bet/(bet+pot) where bet is the bet size that you’re shoving and pot is the pot size before you shove. The alpha value can be extremely useful in certain situations, and we covered one of those situations last week.

The Alpha Value Strikes Again

The unexploitable folding frequency (aka the alpha value) is a percentage. Take that percentage of the size of your unexploitable value betting range and the result is the size of your unexploitable bluffing range. From last week’s column:

So for example, if you had a $10 pot with a $7.50 bet size, then bet/(bet+pot) is 42.9 percent. The size of your unexploitable bluffing range will be 42.9 percent of the size of your unexploitable value betting range. If you decide that your unexploitable value betting range is about 28 combinations, then your unexploitable bluffing range will consist of about 42.9 percent of that which comes to 12 combinations.

What this means is that you only actually need to remember the last three numbers on the chart above: .33, .40 and .50. These correspond to the alpha values for a bet that is about 1/2 pot, a bet that’s about 2/3 to 3/4 pot, and a bet that’s about the size of the pot.

Using This at the Table

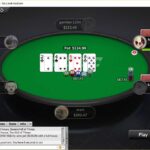
Let’s look at a quick example of how this could work in a real hand. TheLongGrind posted a hand earlier this week where he arrived on the river with a pot worth $23.05 and $13.60 left behind in a heads-up scenario. The bet value here is $13.60, and the pot value is $23.05. The bet size is somewhere around 60 percent of the pot, but it’s not important to be very exact with this at the table as long as you’re in the ballpark.

TheLongGrind checked to his opponent, and his opponent shoved.

The folding frequency is all we really care about. Since the folding frequency for a 1/2-pot bet is .33 and the folding frequency for 2/3-pot bet is .40, then we can estimate that the unexploitable folding frequency in this scenario is probably somewhere in the 36-37 percent range or so since that’s about half-way between those values. We have to decide to fold more or less often than that based on a number of factors like what our range looks like, if he’s bluffing more or less than the unexploitable rate and if he’s value betting more or less than the unexploitable rate.

Note that this also tells us that our Villain is bluffing an unexploitable rate when he is bluffing about 36-37 percent as often as he is value betting. We should use this as the reference point to decide if his bluffing rate compels us to call more or less than the unexploitable rate.

Thinking With Game Theory

What you’ll notice is that this type of thinking has us worrying more about our entire range than our individual hand. Instead of thinking, “What should I do with hand X here?” we are thinking, “What should I do with my range here?” While it’s important to realize what’s going on with your individual hand, thinking deeply about your range is a key aspect of being a good hold’em player.