Zeebo's Theorem - Nobody ever folded a
full house.
Reasoning: Nobody is good enough to
fold a
monster. Most players aren't even good enough to
fold a hand that looks like a
monster but really isn't.
Application: There are two basic applications to this theory. The first is that if you put your opponent on a
full house and you can beat them,
don't be afraid to
overbet/
push the
river. This is particularly true when there is
three of a kind on the board. Players will
call with an incredible
range of full houses in that
spot. It is true that some
villain may
fold 22 on a board with three aces. However, you have no way of knowing if they have 22 or
TT so go
ahead and
felt them. You are losing value if you
don't. And sometimes they'll
call with 22 anyway.
The second thing to realize is to never try to
bluff anyone off a
full house. If you have 22 on a board with three Aces,
don't expect to be
able to
push 66 off his hand.
This theorem also generally applies to any
monster over
monster situation, from
straight flush over
quads/FH/nut
flush down to
set over set.
Reliability: This is the most reliable theorem. Nearly 100%. Somebody will
post and argue that it is actually 100%.
Reference:
http://captzeebo.supok.net/2006-02-12.html
Clarkmeister's Theorem - When you are OOP HU on the
river and a 4-
flush comes always bet.
Reasoning: Simply put, a 4-
flush is an ideal bluffing situation.
Application: Bet a lot of 4-flushes, particularly HU, OOP on the
river. You will get a ton of folds. Most everyone is folding non-
flush hands (that beat you) and small flushes.
Reliability: Yes, sometimes
villain has the nut
flush or calls with the K-high
flush. Nothing you can do there. But over the long haul this is a VERY profitable
spot to
bluff.
Keep in mind though, you ARE turning your hand into a
bluff. If you have a hand you
don't want to
turn into a bluff (very
villain dependent) like
top set or the K-high
flush then
check/calling can be fine.
BelugaWhale Theorem - When you are the preflop raiser and your
turn bet is raised or
check/
raise, it is time to re-evaluate
one pair hands.
Reasoning: In raised pots, most players will just
call down with
one pair (be it
pocket pair or
top pair) type hands as
well as draws. The
turn is where most players who flopped a
monster stop slowplaying and try to build pot. Or, they
raise if they hit their
draw.
Application: A
raise on the
turn is a signal to re-evaluate where you are at. It is not and automatic
fold but you need to consider if
villain has a
monster or just hit his
draw.
Reliability: Against
fish and bad players in general, with the exception sometimes of LAGs and maniacs, this is a VERY reliably theorem. However, it is also an extremely popular and
well known theorem, perhaps the best known. A lot of good players, particularly 2+2 players can try to
exploit this theorem, especially by floating. So depending on the player (a decent player who is ALSO capable of making a play) you may need to
discount this theorem considerably.
Yeti Theorem - A
flop three bet on a dry (preferably paired) board is always a
bluff.
Reasoning: On a paired (or otherwise very
dry flop) a player with an
overpair is unlikely to want to
stack off because usually the only hand he gets
action from is a
monster that crushes him. For this reason, someone who DOES have a
monster usually will usually slowplay here. Since neither strong hands like
top pair and overpairs
don't 3bet here and monsters
don't 3bet here the only hands left that 3bet are bluffs.
Application: If someone 3bets you in this situation, 4bet/
push.
Reliability: These days this is mostly considered a joke theorem or a sarcastic excuse for
spew. This is because Internet games between regulars are so much more aggressive than pre-Internet (ie live) games. For many players, "fast play is the new
slow play" so players will
stack off in these spots both with overpairs AND with monsters.
Aggression is often used to conceal hand strength as much or more as slowplaying is used.
Against some players (ABC
TAG) this theorem does still hold merit however.





 Reply With Quote
Reply With Quote



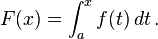 Then, F is continuous on [a, b], differentiable on the
Then, F is continuous on [a, b], differentiable on the  for all x in (a, b).
for all x in (a, b). Then
Then 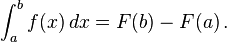 .
.











